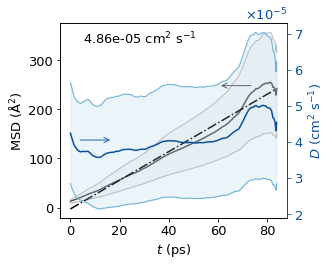
MSD and diffusion coefficient

Import packages

from fishmol import trj, msd
from cage_data import cage1_info
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from fishmol import style

Import information of the simulated system

# The simulation box
cell = cage1_info.cell
# Waters is a dict contains the indices of atoms of water molcules
waters = cage1_info.waters
water_indices = [[*water.values()] for water in waters]
print(water_indices)

[[14, 15, 16], [17, 18, 19], [143, 144, 145], [146, 147, 148], [272, 273, 274], [275, 276, 277], [401, 402, 403], [404, 405, 406]]

Read trajectory data file

%%time
# The trajectory is a large file (517 MB)
traj = trj.Trajectory(timestep = 5, data = "/nobackup/rhtp48/data_ana/fishmol_examples/cage_data/cage1-500K.xyz", index = ":", cell = cell)

CPU times: user 45.4 s, sys: 1.47 s, total: 46.9 s
Wall time: 47.1 s

You can retrieve and confirm the simulation cell info

traj.cell

[[21.2944, 0.0, 0.0],
 [-4.6030371123, 20.7909480472, 0.0],
 [-0.9719093466, -1.2106211379, 15.1054299403]]

A test of calc_com() function is working

traj.frames[0][water_indices[0]].calc_com()

array([10.58631557, 19.90213351, 10.38000923])

Calculate the centre of masses (CoMs) for water molecules

from fishmol.utils import update_progress # import the progress bar function

water_coms = np.zeros((traj.nframes, 3*len(water_indices)))

for i, frame in enumerate(traj.frames):
    # Calculate com
    coms = [frame[water_idx].calc_com() for water_idx in water_indices]
    water_coms[i] = np.asarray(coms).flatten()
    update_progress(i/traj.nframes)
    
# Add data to dateframe
columns=[]
for i in range(1, len(water_indices) + 1):
    columns += [f"water{i}_x", f"water{i}_y", f"water{i}_z"]

water_com_df = pd.DataFrame(columns=columns, data = water_coms)

# Write data to excel file
water_com_df.to_excel("test/cage1-500K-water-com.xlsx")
update_progress(1)

Progress: [■■■■■■■■■■■■■■■■■■■■] 100.0%

water_com_df.head()

	water1_x	water1_y	water1_z	water2_x	water2_y	water2_z	water3_x	water3_y	water3_z	water4_x	...	water5_z	water6_x	water6_y	water6_z	water7_x	water7_y	water7_z	water8_x	water8_y	water8_z
0	10.586316	19.902134	10.380009	0.624155	10.923925	8.298079	-1.967392	4.261146	12.241481	4.693672	...	4.725172	15.090375	8.649502	6.883228	17.759366	15.321196	2.865725	11.019290	3.578953	0.703805
1	10.597616	19.945151	10.393126	0.617881	10.942585	8.312331	-1.961926	4.253910	12.205821	4.689873	...	4.745156	15.076014	8.640429	6.849210	17.749958	15.278667	2.889409	11.049146	3.587807	0.663123
2	10.610208	20.003821	10.408405	0.610859	10.967922	8.330438	-1.953047	4.243309	12.156421	4.687198	...	4.767198	15.058083	8.628816	6.804086	17.738720	15.225162	2.920655	11.086905	3.600664	0.608757
3	10.622718	20.062112	10.416761	0.604688	10.993416	8.349495	-1.945208	4.229969	12.106099	4.687512	...	4.786539	15.040753	8.617851	6.760128	17.728982	15.181476	2.948253	11.122864	3.614650	0.558271
4	10.636664	20.122749	10.416813	0.597829	11.020753	8.373153	-1.941190	4.211549	12.054352	4.691621	...	4.808036	15.020218	8.605213	6.714651	17.717884	15.151479	2.970079	11.155729	3.629731	0.511643

5 rows × 24 columns

del water_coms

Calculate the mean squared displacement of water molecules

Create the time data

start_idx = 0
t0 = start_idx * 5
t_end = t0 + 5*(len(water_com_df)-1) # 5 fs is the interval of traj
t = np.linspace(t0, t_end, num = len(water_com_df))

msd_d_df = pd.DataFrame()
msd_d_df["t"] = t[1:]

Calculate the MSD and D

Define a function to calculate the mean squre displacements (MSDs).

The mean squared displacement (MSD) measures how much particles move over time. There are a number of definitions for the mean squared displacement. The MSDs here are calculated from the most common form, which is defined as: $\( MSD(m) = \frac{1}{N_{particles}} \sum_{i=1}^{N_{particles}} \frac{1}{N-m} \sum_{k=0}^{N-m-1} (\vec{r}_i(k+m) - \vec{r}_i(k))^2 \)\( where \)r_i(k)\( is the position of particle \)i\( in frame \)k\(. The mean squared displacement is averaged displacements over all windows of length \)m$. The algorithm used is described in calandrini2011nmoldyn which can be realised by the code in this StackOverflow thread.

for i in range(len(water_indices)):
    temp = np.array(water_com_df.iloc[:, 3*i:3*i+3])
    msds = msd.msd_fft(temp)
    msd_d_df[f"water{i}_MSD"] = msds[1:]
    msd_d_df[f"water{i}_D"] = msds[1:] * 1E-16 / (6*t[1:]*1E-15)

msd_df = msd_d_df.iloc[:, 1:16:2]
d_df = msd_d_df.iloc[:, 2:17:2]

Calculate average values of MSD and D

msd_d_df["Mean_MSD"] = msd_df.mean(axis=1)
msd_d_df["MSD_error"] = msd_df.std(axis=1) / 8**0.5
msd_d_df["Mean_D"] = d_df.mean(axis=1)
msd_d_df["D_error"] = d_df.std(axis=1) / 8**0.5

# Save the data
msd_d_df.to_excel("test/cage1-H2O-MSD-D-500K.xlsx")

Plot the data

# skip the first 5 ps, that the system is still equilibrating
msd_d_df = msd_d_df.iloc[1000:,:]
msd_d_df["t"] = (msd_d_df["t"] -5000)
msd_d_df.head()

	t	water0_MSD	water0_D	water1_MSD	water1_D	water2_MSD	water2_D	water3_MSD	water3_D	water4_MSD	...	water5_MSD	water5_D	water6_MSD	water6_D	water7_MSD	water7_D	Mean_MSD	MSD_error	Mean_D	D_error
1000	5.0	4.093919	0.000014	19.722342	0.000066	2.003004	0.000007	33.566337	0.000112	1.458750	...	19.347635	0.000064	2.614106	0.000009	19.172680	0.000064	12.747347	4.198995	0.000042	0.000014
1001	10.0	4.095739	0.000014	19.746275	0.000066	2.003836	0.000007	33.597794	0.000112	1.458538	...	19.358398	0.000064	2.613060	0.000009	19.178147	0.000064	12.756473	4.202892	0.000042	0.000014
1002	15.0	4.097586	0.000014	19.770177	0.000066	2.004774	0.000007	33.629258	0.000112	1.458261	...	19.369117	0.000064	2.612067	0.000009	19.183779	0.000064	12.765627	4.206788	0.000042	0.000014
1003	20.0	4.099463	0.000014	19.794038	0.000066	2.005816	0.000007	33.660730	0.000112	1.457916	...	19.379795	0.000064	2.611117	0.000009	19.189575	0.000064	12.774806	4.210683	0.000042	0.000014
1004	25.0	4.101374	0.000014	19.817852	0.000066	2.006957	0.000007	33.692212	0.000112	1.457499	...	19.390432	0.000064	2.610204	0.000009	19.195537	0.000064	12.784008	4.214578	0.000042	0.000014

5 rows × 21 columns

fig = plt.figure(figsize=(4.6,3.6))
ax  = fig.add_axes([0.16, 0.16, 0.685, 0.75])

color = "#08519c"
ax.plot(msd_d_df["t"]/1000, msd_d_df["Mean_MSD"], color = "#525252")

ax.plot(msd_d_df["t"]/1000, msd_d_df["Mean_MSD"] - msd_d_df["MSD_error"], linewidth = 1, color = "#bdbdbd")
ax.plot(msd_d_df["t"]/1000, msd_d_df["Mean_MSD"] + msd_d_df["MSD_error"], linewidth = 1, color = "#bdbdbd")

ax.fill_between(msd_d_df["t"]/1000, msd_d_df["Mean_MSD"] + msd_d_df["MSD_error"], msd_d_df["Mean_MSD"] - msd_d_df["MSD_error"], color= "#d9d9d9", alpha = 0.2)

linear_model = np.polyfit(msd_d_df["t"]/1000, msd_d_df["Mean_MSD"],1)  
linear_model_fn = np.poly1d(linear_model) 

x_s = np.arange(msd_d_df["t"].min()/1000, msd_d_df["t"].max()/1000)  
ax.plot(x_s,linear_model_fn(x_s), color="k", ls ="-.")

ax1 = ax.twinx()
ax1.plot(msd_d_df["t"]/1000, msd_d_df["Mean_D"], color = color)
ax1.plot(msd_d_df["t"]/1000, msd_d_df["Mean_D"] - msd_d_df["D_error"], linewidth = 1, color = "#6baed6")
ax1.plot(msd_d_df["t"]/1000, msd_d_df["Mean_D"] + msd_d_df["D_error"], linewidth = 1, color = "#6baed6")

ax1.fill_between(msd_d_df["t"]/1000, msd_d_df["Mean_D"] + msd_d_df["D_error"], msd_d_df["Mean_D"] - msd_d_df["D_error"], color = "#9ecae1", alpha = 0.2)

ax.annotate("", xy=(0.7, 0.68), xycoords = "axes fraction",
            xytext=(0.85, 0.68), textcoords='axes fraction',
            arrowprops=dict(arrowstyle="->", color = "#525252"))

ax.annotate("", xy=(0.23, 0.40), xycoords = "axes fraction",
            xytext=(0.08, 0.40), textcoords='axes fraction',
            arrowprops=dict(arrowstyle="->", color = color))

xmin, xmax = ax.get_xlim()
ymin, ymax = ax.get_ylim()

ax.text(xmin + 0.35*(xmax-xmin), ymin + 0.92*(ymax - ymin), "%.2e cm$^2$ s$^{-1}$"%(linear_model[0]/60000), ha = "center", va = "center")

ax.set_ylabel('MSD (Å$^2$)')
ax.set_xlabel('$t$ (ps)')

ax1.set_ylabel('$D$ (cm$^2$ s$^{-1}$)', color = color)
ax1.tick_params(axis='y', color = color, labelcolor = color)
ax1.spines['right'].set_color(color)
ax1.ticklabel_format(axis='y', style='sci', scilimits=[-4,4], useMathText=True)

plt.savefig("test/cage1-ave_msd-d-500K.jpg", dpi =600)

plt.show()